Week 7: Digital Elevation Models

The area that I selected is in the Los Angeles region. The extent of the area, in decimal degrees is 119.409 W to 118.824 W, and 34.438 N to 34.827 N. The geographic coordinate system is North American Datum 1983 (UTM Zone 11). The region I chose is hilly in its topography, as easily seen by the 3-D models below. By looking at the aspect map, it can be seen that a lot of the land faces north/south rather than east/west. The slope of the hills is relatively gentle, except at the peaks (shown by red areas on the slope map). The hillshade map gives a good picture of the general terrain. I included the 3-D images from two different angles to give a greater picture about what the region generally looks like.

Week 6: Map Projections

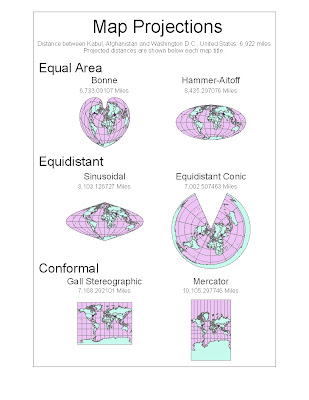
Map projections are necessary because a three dimensional sphere, like Earth, cannot be flawlessly represented on a two dimensional map. When we try to represent the Earth on a flat surface, distortions occur which could be deceiving to the map reader. However, maps are able to preserve certain features, such as direction, distance, or area. This makes particular maps better for specific purposes than others. Three map projection categories that I have included in my ArcGIS project are equal area, equidistant, and conformal. Depending on what the map is being used for, each of these categories could be beneficial. When looking at the distance between two cities, such as between Washington D.C. and Kabul, Afghanistan in my project, different results will be yielded based on the type of projection used. Some projections exaggerate the distance by almost double. This is one example of why map projections matter when doing spatial analysis.


The first two maps on my project are equal area projections. An equal area map is made so that one square kilometer drawn on one portion of the map is equal in area to a square kilometer drawn on another portion. The Bonne projection is a pseudoconical equal area map projection. It has a slight heart shape, and on the central meridian and standard latitudes shapes are not distorted. The other equal area map on my project is the Hammer-Aitoff. Hammer created this equal area map based on Aitoff’s equidistant map. One aspect of the significance of an equal area map is that it does not exaggerate the sizes of continents relative to each other. This could be important because for political purposes, political leaders could choose a map projection which makes their country look gigantic compared to another country, when in reality the countries are close to the same size. It could be used as propaganda to advocate going to war against another country. Thus, the map projection could be purposely used to deceive the viewer. When relative area is an important aspect of a map, an equal area projection is a useful tool.


The next map projections are equidistant, a map that is centered so that any distance from the central given point is an accurate representation of the distance from that point. Distance is not preserved from any point on the map, but only to the one or two control points. One type of map projection that can be classified as equidistant is the Sinusoidal projection. This is equidistant in the respect that the true distance between two points on the same meridian corresponds to the distance on the map between the two parallels. Another equidistant projection is the equidistant conic projection. On this map the meridians are all equidistant, straight lines which converge at a point, and parallels are arcs of circle, in which distortion is constant along the arc. One significant feature of an equidistant map is that you can compare your distance to other places on the Earth, if you were located at a control point on the map. This could be helpful in determining the shortest route to take if you were on an airplane. Equidistant maps in my project were fairly accurate in projecting the distance from Washington D.C. to Kabul, Afghanistan, even though neither city was a control point on the map. The equidistant conic projection gave the most accurate distance between the two cities of any projection featured in my project.


The final map type represented in my projection is conformal. On conformal maps, angles are preserved locally. This means that a small area can be rendered in its true shape. These maps use grids of longitude and latitude. They do not preserve area or distance, but give a good general picture of the Earth. One example is the Gall Stereographic projection. While temperate countries are shown well on this projection, its vertical stretch creates a large amount of distortion at the poles. This would make this map a poor choice for analyzing how much remaining habitat there is for polar bears. Another example is the Mercator projection, which also greatly distorts the size of land near the poles. The significance of this map is that it is useful for nautical purposes due to its ability to preserve local angles. The linear scale is constant in all directions around a point.


The map projection that is most useful for a specific purpose depends on what is trying to be shown by the map. Equal area, equidistant, and conformal map projections are all useful for certain purposes, but can be misleading if used for other purposes due to distortion. In order to determine the utility of a map, we must be able to understand the implications of the distortions. While these distortions may be dismissible on a small scale, when looking at the world as a whole the distortions are magnitudes larger. By looking at the distance between Washington D.C. and Kabul, Afghanistan on each map projection, it is clear that the distortions really do matter.

Week 4: GIS Data Models

The ArcGIS tutorial takes the user through many of the features available on the program. While it gives the user the freedom to analyze spatial data, many of the features are not intuitive and the user is therefore limited by the program’s complexity. Yet undoubtedly, the potential of GIS is huge. Because it allows its user to store, edit, and create data, it brings us to a new age of information sharing. The main pitfall of the software that I observe is that it is not easy to use for the untrained geographer.
GIS gives people the ability to create maps without having to perform repetitive work. It stores information such as population density, county borders, and school locations so that each geographer making a map of a particular area does not have to start over and collect information all over again. It gives users the ability to build off information already input into the program, while leaving creative freedom to the individual. As more and more information is acquired, GIS becomes very important. It gives us a way of analyzing this data. Population density is important to analyze when deciding where to place community resources such as hospitals and fire departments. GIS can help us decide how to allocate resources in the most spatially effective way.
Another great area of potential in GIS is that we are able to see relationships and correlations by plotting data on the same map. This is applicable to many fields and careers. An example is compiling a map to judge environmental justice in a region. This may consist of a map layered with pollution information and with the race of people living in the region. This type of spatial analysis allows us to determine when environmental injustice is occurring, giving us the possibility to better address it. It would obviously be best if no one had to live in pollution, but unfortunately there is not so much environmental equity in reality. Certain neighborhoods bear the brunt of our pollution, and it is only by comparing these areas spatially to other areas that we can pinpoint these problems. GIS therefore gives us greater understanding of spatial relations so we can make sensible decisions.
However, GIS does have its pitfalls. Unlike neogeography, GIS is map-centric. Neogeography is friendly to the user, and the average person is able to easily create and use maps in new ways. GIS, on the other hand, requires training. While the tools desired by the user may be available through the program, if the user is unable to access these features then it is useless. GIS also has the potential to make the user think they are seeing the “whole picture” when looking at a region, when in reality key information may be missing. An example is that if an elementary school was placed in a region because the population density was relatively high but there was an absence of schools in the area, the school may not be needed because the majority of the population in the region may be past retirement age. Therefore, a flaw in GIS is that it may seem to be representing all the important features of a region, but in reality could be excluding very important data.
When going through the tutorial for the 4th or 5th time, I felt like I was getting a firm grasp on the program ArcGIS. I am comfortable with the main tools and feel that I would be able to do spatial analysis regarding any of the features in the tutorial. However, I do feel that I am limited in my knowledge to what was included in the tutorial. If I had to do spatial analysis in a rural area, I might not be prepared. When something went wrong in the tutorial and I couldn’t click “Undo”, I had no way of troubleshooting the error. The problem comes down to this fact: Using GIS is a skill that must be learned and practiced to be effective. The tutorial is easy to follow and is a great algorithm for making the specified map, but even after thoroughly reviewing the tutorial, the user has barely even tapped the surface of the capabilities of the program. So, while GIS has clear potential to make astonishing leaps in information technology, the pitfall is that its success is limited by the number of people who can use it.